GUIDE to Worksheet 2.2
Contents
GUIDE to Worksheet 2.2#
This notebook is meant to provide hints and guidance on how to complete Worksheet 2.2: An introduction to OLS linear regression. It will not necessarily answer every part of every problem, but it will get you to the interesting points of the worksheet.
Also, these guides may be useful for you as you are building up your coding toolkit to see different ways to execute different tasks in Python. I am not necessarily showing the most efficient or elegant code, but trying to illustrate different ways to do things. You should always use the code you feel you can understand best.
First, let’s take care of our imported modules.
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as st
import seaborn as sns
## Note the modified import statement to only import one thing from the module.
from sklearn.linear_model import LinearRegression as skLinReg
import statsmodels.api as sm
sns.set(color_codes=True)
%matplotlib inline
Part 1#
Use the help function to look at the documentation for each of the 4 functions above.
help(np.polyfit)
Help on function polyfit in module numpy:
polyfit(x, y, deg, rcond=None, full=False, w=None, cov=False)
Least squares polynomial fit.
.. note::
This forms part of the old polynomial API. Since version 1.4, the
new polynomial API defined in `numpy.polynomial` is preferred.
A summary of the differences can be found in the
:doc:`transition guide </reference/routines.polynomials>`.
Fit a polynomial ``p(x) = p[0] * x**deg + ... + p[deg]`` of degree `deg`
to points `(x, y)`. Returns a vector of coefficients `p` that minimises
the squared error in the order `deg`, `deg-1`, ... `0`.
The `Polynomial.fit <numpy.polynomial.polynomial.Polynomial.fit>` class
method is recommended for new code as it is more stable numerically. See
the documentation of the method for more information.
Parameters
----------
x : array_like, shape (M,)
x-coordinates of the M sample points ``(x[i], y[i])``.
y : array_like, shape (M,) or (M, K)
y-coordinates of the sample points. Several data sets of sample
points sharing the same x-coordinates can be fitted at once by
passing in a 2D-array that contains one dataset per column.
deg : int
Degree of the fitting polynomial
rcond : float, optional
Relative condition number of the fit. Singular values smaller than
this relative to the largest singular value will be ignored. The
default value is len(x)*eps, where eps is the relative precision of
the float type, about 2e-16 in most cases.
full : bool, optional
Switch determining nature of return value. When it is False (the
default) just the coefficients are returned, when True diagnostic
information from the singular value decomposition is also returned.
w : array_like, shape (M,), optional
Weights. If not None, the weight ``w[i]`` applies to the unsquared
residual ``y[i] - y_hat[i]`` at ``x[i]``. Ideally the weights are
chosen so that the errors of the products ``w[i]*y[i]`` all have the
same variance. When using inverse-variance weighting, use
``w[i] = 1/sigma(y[i])``. The default value is None.
cov : bool or str, optional
If given and not `False`, return not just the estimate but also its
covariance matrix. By default, the covariance are scaled by
chi2/dof, where dof = M - (deg + 1), i.e., the weights are presumed
to be unreliable except in a relative sense and everything is scaled
such that the reduced chi2 is unity. This scaling is omitted if
``cov='unscaled'``, as is relevant for the case that the weights are
w = 1/sigma, with sigma known to be a reliable estimate of the
uncertainty.
Returns
-------
p : ndarray, shape (deg + 1,) or (deg + 1, K)
Polynomial coefficients, highest power first. If `y` was 2-D, the
coefficients for `k`-th data set are in ``p[:,k]``.
residuals, rank, singular_values, rcond
These values are only returned if ``full == True``
- residuals -- sum of squared residuals of the least squares fit
- rank -- the effective rank of the scaled Vandermonde
coefficient matrix
- singular_values -- singular values of the scaled Vandermonde
coefficient matrix
- rcond -- value of `rcond`.
For more details, see `numpy.linalg.lstsq`.
V : ndarray, shape (M,M) or (M,M,K)
Present only if ``full == False`` and ``cov == True``. The covariance
matrix of the polynomial coefficient estimates. The diagonal of
this matrix are the variance estimates for each coefficient. If y
is a 2-D array, then the covariance matrix for the `k`-th data set
are in ``V[:,:,k]``
Warns
-----
RankWarning
The rank of the coefficient matrix in the least-squares fit is
deficient. The warning is only raised if ``full == False``.
The warnings can be turned off by
>>> import warnings
>>> warnings.simplefilter('ignore', np.RankWarning)
See Also
--------
polyval : Compute polynomial values.
linalg.lstsq : Computes a least-squares fit.
scipy.interpolate.UnivariateSpline : Computes spline fits.
Notes
-----
The solution minimizes the squared error
.. math::
E = \sum_{j=0}^k |p(x_j) - y_j|^2
in the equations::
x[0]**n * p[0] + ... + x[0] * p[n-1] + p[n] = y[0]
x[1]**n * p[0] + ... + x[1] * p[n-1] + p[n] = y[1]
...
x[k]**n * p[0] + ... + x[k] * p[n-1] + p[n] = y[k]
The coefficient matrix of the coefficients `p` is a Vandermonde matrix.
`polyfit` issues a `RankWarning` when the least-squares fit is badly
conditioned. This implies that the best fit is not well-defined due
to numerical error. The results may be improved by lowering the polynomial
degree or by replacing `x` by `x` - `x`.mean(). The `rcond` parameter
can also be set to a value smaller than its default, but the resulting
fit may be spurious: including contributions from the small singular
values can add numerical noise to the result.
Note that fitting polynomial coefficients is inherently badly conditioned
when the degree of the polynomial is large or the interval of sample points
is badly centered. The quality of the fit should always be checked in these
cases. When polynomial fits are not satisfactory, splines may be a good
alternative.
References
----------
.. [1] Wikipedia, "Curve fitting",
https://en.wikipedia.org/wiki/Curve_fitting
.. [2] Wikipedia, "Polynomial interpolation",
https://en.wikipedia.org/wiki/Polynomial_interpolation
Examples
--------
>>> import warnings
>>> x = np.array([0.0, 1.0, 2.0, 3.0, 4.0, 5.0])
>>> y = np.array([0.0, 0.8, 0.9, 0.1, -0.8, -1.0])
>>> z = np.polyfit(x, y, 3)
>>> z
array([ 0.08703704, -0.81349206, 1.69312169, -0.03968254]) # may vary
It is convenient to use `poly1d` objects for dealing with polynomials:
>>> p = np.poly1d(z)
>>> p(0.5)
0.6143849206349179 # may vary
>>> p(3.5)
-0.34732142857143039 # may vary
>>> p(10)
22.579365079365115 # may vary
High-order polynomials may oscillate wildly:
>>> with warnings.catch_warnings():
... warnings.simplefilter('ignore', np.RankWarning)
... p30 = np.poly1d(np.polyfit(x, y, 30))
...
>>> p30(4)
-0.80000000000000204 # may vary
>>> p30(5)
-0.99999999999999445 # may vary
>>> p30(4.5)
-0.10547061179440398 # may vary
Illustration:
>>> import matplotlib.pyplot as plt
>>> xp = np.linspace(-2, 6, 100)
>>> _ = plt.plot(x, y, '.', xp, p(xp), '-', xp, p30(xp), '--')
>>> plt.ylim(-2,2)
(-2, 2)
>>> plt.show()
help(st.linregress)
Help on function linregress in module scipy.stats._stats_mstats_common:
linregress(x, y=None, alternative='two-sided')
Calculate a linear least-squares regression for two sets of measurements.
Parameters
----------
x, y : array_like
Two sets of measurements. Both arrays should have the same length. If
only `x` is given (and ``y=None``), then it must be a two-dimensional
array where one dimension has length 2. The two sets of measurements
are then found by splitting the array along the length-2 dimension. In
the case where ``y=None`` and `x` is a 2x2 array, ``linregress(x)`` is
equivalent to ``linregress(x[0], x[1])``.
alternative : {'two-sided', 'less', 'greater'}, optional
Defines the alternative hypothesis. Default is 'two-sided'.
The following options are available:
* 'two-sided': the slope of the regression line is nonzero
* 'less': the slope of the regression line is less than zero
* 'greater': the slope of the regression line is greater than zero
.. versionadded:: 1.7.0
Returns
-------
result : ``LinregressResult`` instance
The return value is an object with the following attributes:
slope : float
Slope of the regression line.
intercept : float
Intercept of the regression line.
rvalue : float
The Pearson correlation coefficient. The square of ``rvalue``
is equal to the coefficient of determination.
pvalue : float
The p-value for a hypothesis test whose null hypothesis is
that the slope is zero, using Wald Test with t-distribution of
the test statistic. See `alternative` above for alternative
hypotheses.
stderr : float
Standard error of the estimated slope (gradient), under the
assumption of residual normality.
intercept_stderr : float
Standard error of the estimated intercept, under the assumption
of residual normality.
See Also
--------
scipy.optimize.curve_fit :
Use non-linear least squares to fit a function to data.
scipy.optimize.leastsq :
Minimize the sum of squares of a set of equations.
Notes
-----
Missing values are considered pair-wise: if a value is missing in `x`,
the corresponding value in `y` is masked.
For compatibility with older versions of SciPy, the return value acts
like a ``namedtuple`` of length 5, with fields ``slope``, ``intercept``,
``rvalue``, ``pvalue`` and ``stderr``, so one can continue to write::
slope, intercept, r, p, se = linregress(x, y)
With that style, however, the standard error of the intercept is not
available. To have access to all the computed values, including the
standard error of the intercept, use the return value as an object
with attributes, e.g.::
result = linregress(x, y)
print(result.intercept, result.intercept_stderr)
Examples
--------
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import stats
>>> rng = np.random.default_rng()
Generate some data:
>>> x = rng.random(10)
>>> y = 1.6*x + rng.random(10)
Perform the linear regression:
>>> res = stats.linregress(x, y)
Coefficient of determination (R-squared):
>>> print(f"R-squared: {res.rvalue**2:.6f}")
R-squared: 0.717533
Plot the data along with the fitted line:
>>> plt.plot(x, y, 'o', label='original data')
>>> plt.plot(x, res.intercept + res.slope*x, 'r', label='fitted line')
>>> plt.legend()
>>> plt.show()
Calculate 95% confidence interval on slope and intercept:
>>> # Two-sided inverse Students t-distribution
>>> # p - probability, df - degrees of freedom
>>> from scipy.stats import t
>>> tinv = lambda p, df: abs(t.ppf(p/2, df))
>>> ts = tinv(0.05, len(x)-2)
>>> print(f"slope (95%): {res.slope:.6f} +/- {ts*res.stderr:.6f}")
slope (95%): 1.453392 +/- 0.743465
>>> print(f"intercept (95%): {res.intercept:.6f}"
... f" +/- {ts*res.intercept_stderr:.6f}")
intercept (95%): 0.616950 +/- 0.544475
help(skLinReg)
Help on class LinearRegression in module sklearn.linear_model._base:
class LinearRegression(sklearn.base.MultiOutputMixin, sklearn.base.RegressorMixin, LinearModel)
| LinearRegression(*, fit_intercept=True, copy_X=True, n_jobs=None, positive=False)
|
| Ordinary least squares Linear Regression.
|
| LinearRegression fits a linear model with coefficients w = (w1, ..., wp)
| to minimize the residual sum of squares between the observed targets in
| the dataset, and the targets predicted by the linear approximation.
|
| Parameters
| ----------
| fit_intercept : bool, default=True
| Whether to calculate the intercept for this model. If set
| to False, no intercept will be used in calculations
| (i.e. data is expected to be centered).
|
| copy_X : bool, default=True
| If True, X will be copied; else, it may be overwritten.
|
| n_jobs : int, default=None
| The number of jobs to use for the computation. This will only provide
| speedup in case of sufficiently large problems, that is if firstly
| `n_targets > 1` and secondly `X` is sparse or if `positive` is set
| to `True`. ``None`` means 1 unless in a
| :obj:`joblib.parallel_backend` context. ``-1`` means using all
| processors. See :term:`Glossary <n_jobs>` for more details.
|
| positive : bool, default=False
| When set to ``True``, forces the coefficients to be positive. This
| option is only supported for dense arrays.
|
| .. versionadded:: 0.24
|
| Attributes
| ----------
| coef_ : array of shape (n_features, ) or (n_targets, n_features)
| Estimated coefficients for the linear regression problem.
| If multiple targets are passed during the fit (y 2D), this
| is a 2D array of shape (n_targets, n_features), while if only
| one target is passed, this is a 1D array of length n_features.
|
| rank_ : int
| Rank of matrix `X`. Only available when `X` is dense.
|
| singular_ : array of shape (min(X, y),)
| Singular values of `X`. Only available when `X` is dense.
|
| intercept_ : float or array of shape (n_targets,)
| Independent term in the linear model. Set to 0.0 if
| `fit_intercept = False`.
|
| n_features_in_ : int
| Number of features seen during :term:`fit`.
|
| .. versionadded:: 0.24
|
| feature_names_in_ : ndarray of shape (`n_features_in_`,)
| Names of features seen during :term:`fit`. Defined only when `X`
| has feature names that are all strings.
|
| .. versionadded:: 1.0
|
| See Also
| --------
| Ridge : Ridge regression addresses some of the
| problems of Ordinary Least Squares by imposing a penalty on the
| size of the coefficients with l2 regularization.
| Lasso : The Lasso is a linear model that estimates
| sparse coefficients with l1 regularization.
| ElasticNet : Elastic-Net is a linear regression
| model trained with both l1 and l2 -norm regularization of the
| coefficients.
|
| Notes
| -----
| From the implementation point of view, this is just plain Ordinary
| Least Squares (scipy.linalg.lstsq) or Non Negative Least Squares
| (scipy.optimize.nnls) wrapped as a predictor object.
|
| Examples
| --------
| >>> import numpy as np
| >>> from sklearn.linear_model import LinearRegression
| >>> X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
| >>> # y = 1 * x_0 + 2 * x_1 + 3
| >>> y = np.dot(X, np.array([1, 2])) + 3
| >>> reg = LinearRegression().fit(X, y)
| >>> reg.score(X, y)
| 1.0
| >>> reg.coef_
| array([1., 2.])
| >>> reg.intercept_
| 3.0...
| >>> reg.predict(np.array([[3, 5]]))
| array([16.])
|
| Method resolution order:
| LinearRegression
| sklearn.base.MultiOutputMixin
| sklearn.base.RegressorMixin
| LinearModel
| sklearn.base.BaseEstimator
| builtins.object
|
| Methods defined here:
|
| __init__(self, *, fit_intercept=True, copy_X=True, n_jobs=None, positive=False)
| Initialize self. See help(type(self)) for accurate signature.
|
| fit(self, X, y, sample_weight=None)
| Fit linear model.
|
| Parameters
| ----------
| X : {array-like, sparse matrix} of shape (n_samples, n_features)
| Training data.
|
| y : array-like of shape (n_samples,) or (n_samples, n_targets)
| Target values. Will be cast to X's dtype if necessary.
|
| sample_weight : array-like of shape (n_samples,), default=None
| Individual weights for each sample.
|
| .. versionadded:: 0.17
| parameter *sample_weight* support to LinearRegression.
|
| Returns
| -------
| self : object
| Fitted Estimator.
|
| ----------------------------------------------------------------------
| Data and other attributes defined here:
|
| __abstractmethods__ = frozenset()
|
| __annotations__ = {'_parameter_constraints': <class 'dict'>}
|
| ----------------------------------------------------------------------
| Data descriptors inherited from sklearn.base.MultiOutputMixin:
|
| __dict__
| dictionary for instance variables (if defined)
|
| __weakref__
| list of weak references to the object (if defined)
|
| ----------------------------------------------------------------------
| Methods inherited from sklearn.base.RegressorMixin:
|
| score(self, X, y, sample_weight=None)
| Return the coefficient of determination of the prediction.
|
| The coefficient of determination :math:`R^2` is defined as
| :math:`(1 - \frac{u}{v})`, where :math:`u` is the residual
| sum of squares ``((y_true - y_pred)** 2).sum()`` and :math:`v`
| is the total sum of squares ``((y_true - y_true.mean()) ** 2).sum()``.
| The best possible score is 1.0 and it can be negative (because the
| model can be arbitrarily worse). A constant model that always predicts
| the expected value of `y`, disregarding the input features, would get
| a :math:`R^2` score of 0.0.
|
| Parameters
| ----------
| X : array-like of shape (n_samples, n_features)
| Test samples. For some estimators this may be a precomputed
| kernel matrix or a list of generic objects instead with shape
| ``(n_samples, n_samples_fitted)``, where ``n_samples_fitted``
| is the number of samples used in the fitting for the estimator.
|
| y : array-like of shape (n_samples,) or (n_samples, n_outputs)
| True values for `X`.
|
| sample_weight : array-like of shape (n_samples,), default=None
| Sample weights.
|
| Returns
| -------
| score : float
| :math:`R^2` of ``self.predict(X)`` w.r.t. `y`.
|
| Notes
| -----
| The :math:`R^2` score used when calling ``score`` on a regressor uses
| ``multioutput='uniform_average'`` from version 0.23 to keep consistent
| with default value of :func:`~sklearn.metrics.r2_score`.
| This influences the ``score`` method of all the multioutput
| regressors (except for
| :class:`~sklearn.multioutput.MultiOutputRegressor`).
|
| ----------------------------------------------------------------------
| Methods inherited from LinearModel:
|
| predict(self, X)
| Predict using the linear model.
|
| Parameters
| ----------
| X : array-like or sparse matrix, shape (n_samples, n_features)
| Samples.
|
| Returns
| -------
| C : array, shape (n_samples,)
| Returns predicted values.
|
| ----------------------------------------------------------------------
| Methods inherited from sklearn.base.BaseEstimator:
|
| __getstate__(self)
| Helper for pickle.
|
| __repr__(self, N_CHAR_MAX=700)
| Return repr(self).
|
| __setstate__(self, state)
|
| get_params(self, deep=True)
| Get parameters for this estimator.
|
| Parameters
| ----------
| deep : bool, default=True
| If True, will return the parameters for this estimator and
| contained subobjects that are estimators.
|
| Returns
| -------
| params : dict
| Parameter names mapped to their values.
|
| set_params(self, **params)
| Set the parameters of this estimator.
|
| The method works on simple estimators as well as on nested objects
| (such as :class:`~sklearn.pipeline.Pipeline`). The latter have
| parameters of the form ``<component>__<parameter>`` so that it's
| possible to update each component of a nested object.
|
| Parameters
| ----------
| **params : dict
| Estimator parameters.
|
| Returns
| -------
| self : estimator instance
| Estimator instance.
help(sm.OLS)
Help on class OLS in module statsmodels.regression.linear_model:
class OLS(WLS)
| OLS(endog, exog=None, missing='none', hasconst=None, **kwargs)
|
| Ordinary Least Squares
|
| Parameters
| ----------
| endog : array_like
| A 1-d endogenous response variable. The dependent variable.
| exog : array_like
| A nobs x k array where `nobs` is the number of observations and `k`
| is the number of regressors. An intercept is not included by default
| and should be added by the user. See
| :func:`statsmodels.tools.add_constant`.
| missing : str
| Available options are 'none', 'drop', and 'raise'. If 'none', no nan
| checking is done. If 'drop', any observations with nans are dropped.
| If 'raise', an error is raised. Default is 'none'.
| hasconst : None or bool
| Indicates whether the RHS includes a user-supplied constant. If True,
| a constant is not checked for and k_constant is set to 1 and all
| result statistics are calculated as if a constant is present. If
| False, a constant is not checked for and k_constant is set to 0.
| **kwargs
| Extra arguments that are used to set model properties when using the
| formula interface.
|
| Attributes
| ----------
| weights : scalar
| Has an attribute weights = array(1.0) due to inheritance from WLS.
|
| See Also
| --------
| WLS : Fit a linear model using Weighted Least Squares.
| GLS : Fit a linear model using Generalized Least Squares.
|
| Notes
| -----
| No constant is added by the model unless you are using formulas.
|
| Examples
| --------
| >>> import statsmodels.api as sm
| >>> import numpy as np
| >>> duncan_prestige = sm.datasets.get_rdataset("Duncan", "carData")
| >>> Y = duncan_prestige.data['income']
| >>> X = duncan_prestige.data['education']
| >>> X = sm.add_constant(X)
| >>> model = sm.OLS(Y,X)
| >>> results = model.fit()
| >>> results.params
| const 10.603498
| education 0.594859
| dtype: float64
|
| >>> results.tvalues
| const 2.039813
| education 6.892802
| dtype: float64
|
| >>> print(results.t_test([1, 0]))
| Test for Constraints
| ==============================================================================
| coef std err t P>|t| [0.025 0.975]
| ------------------------------------------------------------------------------
| c0 10.6035 5.198 2.040 0.048 0.120 21.087
| ==============================================================================
|
| >>> print(results.f_test(np.identity(2)))
| <F test: F=array([[159.63031026]]), p=1.2607168903696672e-20, df_denom=43, df_num=2>
|
| Method resolution order:
| OLS
| WLS
| RegressionModel
| statsmodels.base.model.LikelihoodModel
| statsmodels.base.model.Model
| builtins.object
|
| Methods defined here:
|
| __init__(self, endog, exog=None, missing='none', hasconst=None, **kwargs)
| Initialize self. See help(type(self)) for accurate signature.
|
| fit_regularized(self, method='elastic_net', alpha=0.0, L1_wt=1.0, start_params=None, profile_scale=False, refit=False, **kwargs)
| Return a regularized fit to a linear regression model.
|
| Parameters
| ----------
| method : str
| Either 'elastic_net' or 'sqrt_lasso'.
| alpha : scalar or array_like
| The penalty weight. If a scalar, the same penalty weight
| applies to all variables in the model. If a vector, it
| must have the same length as `params`, and contains a
| penalty weight for each coefficient.
| L1_wt : scalar
| The fraction of the penalty given to the L1 penalty term.
| Must be between 0 and 1 (inclusive). If 0, the fit is a
| ridge fit, if 1 it is a lasso fit.
| start_params : array_like
| Starting values for ``params``.
| profile_scale : bool
| If True the penalized fit is computed using the profile
| (concentrated) log-likelihood for the Gaussian model.
| Otherwise the fit uses the residual sum of squares.
| refit : bool
| If True, the model is refit using only the variables that
| have non-zero coefficients in the regularized fit. The
| refitted model is not regularized.
| **kwargs
| Additional keyword arguments that contain information used when
| constructing a model using the formula interface.
|
| Returns
| -------
| statsmodels.base.elastic_net.RegularizedResults
| The regularized results.
|
| Notes
| -----
| The elastic net uses a combination of L1 and L2 penalties.
| The implementation closely follows the glmnet package in R.
|
| The function that is minimized is:
|
| .. math::
|
| 0.5*RSS/n + alpha*((1-L1\_wt)*|params|_2^2/2 + L1\_wt*|params|_1)
|
| where RSS is the usual regression sum of squares, n is the
| sample size, and :math:`|*|_1` and :math:`|*|_2` are the L1 and L2
| norms.
|
| For WLS and GLS, the RSS is calculated using the whitened endog and
| exog data.
|
| Post-estimation results are based on the same data used to
| select variables, hence may be subject to overfitting biases.
|
| The elastic_net method uses the following keyword arguments:
|
| maxiter : int
| Maximum number of iterations
| cnvrg_tol : float
| Convergence threshold for line searches
| zero_tol : float
| Coefficients below this threshold are treated as zero.
|
| The square root lasso approach is a variation of the Lasso
| that is largely self-tuning (the optimal tuning parameter
| does not depend on the standard deviation of the regression
| errors). If the errors are Gaussian, the tuning parameter
| can be taken to be
|
| alpha = 1.1 * np.sqrt(n) * norm.ppf(1 - 0.05 / (2 * p))
|
| where n is the sample size and p is the number of predictors.
|
| The square root lasso uses the following keyword arguments:
|
| zero_tol : float
| Coefficients below this threshold are treated as zero.
|
| The cvxopt module is required to estimate model using the square root
| lasso.
|
| References
| ----------
| .. [*] Friedman, Hastie, Tibshirani (2008). Regularization paths for
| generalized linear models via coordinate descent. Journal of
| Statistical Software 33(1), 1-22 Feb 2010.
|
| .. [*] A Belloni, V Chernozhukov, L Wang (2011). Square-root Lasso:
| pivotal recovery of sparse signals via conic programming.
| Biometrika 98(4), 791-806. https://arxiv.org/pdf/1009.5689.pdf
|
| hessian(self, params, scale=None)
| Evaluate the Hessian function at a given point.
|
| Parameters
| ----------
| params : array_like
| The parameter vector at which the Hessian is computed.
| scale : float or None
| If None, return the profile (concentrated) log likelihood
| (profiled over the scale parameter), else return the
| log-likelihood using the given scale value.
|
| Returns
| -------
| ndarray
| The Hessian matrix.
|
| hessian_factor(self, params, scale=None, observed=True)
| Calculate the weights for the Hessian.
|
| Parameters
| ----------
| params : ndarray
| The parameter at which Hessian is evaluated.
| scale : None or float
| If scale is None, then the default scale will be calculated.
| Default scale is defined by `self.scaletype` and set in fit.
| If scale is not None, then it is used as a fixed scale.
| observed : bool
| If True, then the observed Hessian is returned. If false then the
| expected information matrix is returned.
|
| Returns
| -------
| ndarray
| A 1d weight vector used in the calculation of the Hessian.
| The hessian is obtained by `(exog.T * hessian_factor).dot(exog)`.
|
| loglike(self, params, scale=None)
| The likelihood function for the OLS model.
|
| Parameters
| ----------
| params : array_like
| The coefficients with which to estimate the log-likelihood.
| scale : float or None
| If None, return the profile (concentrated) log likelihood
| (profiled over the scale parameter), else return the
| log-likelihood using the given scale value.
|
| Returns
| -------
| float
| The likelihood function evaluated at params.
|
| score(self, params, scale=None)
| Evaluate the score function at a given point.
|
| The score corresponds to the profile (concentrated)
| log-likelihood in which the scale parameter has been profiled
| out.
|
| Parameters
| ----------
| params : array_like
| The parameter vector at which the score function is
| computed.
| scale : float or None
| If None, return the profile (concentrated) log likelihood
| (profiled over the scale parameter), else return the
| log-likelihood using the given scale value.
|
| Returns
| -------
| ndarray
| The score vector.
|
| whiten(self, x)
| OLS model whitener does nothing.
|
| Parameters
| ----------
| x : array_like
| Data to be whitened.
|
| Returns
| -------
| array_like
| The input array unmodified.
|
| See Also
| --------
| OLS : Fit a linear model using Ordinary Least Squares.
|
| ----------------------------------------------------------------------
| Methods inherited from RegressionModel:
|
| fit(self, method: "Literal['pinv', 'qr']" = 'pinv', cov_type: "Literal['nonrobust', 'fixed scale', 'HC0', 'HC1', 'HC2', 'HC3', 'HAC', 'hac-panel', 'hac-groupsum', 'cluster']" = 'nonrobust', cov_kwds=None, use_t: 'bool | None' = None, **kwargs)
| Full fit of the model.
|
| The results include an estimate of covariance matrix, (whitened)
| residuals and an estimate of scale.
|
| Parameters
| ----------
| method : str, optional
| Can be "pinv", "qr". "pinv" uses the Moore-Penrose pseudoinverse
| to solve the least squares problem. "qr" uses the QR
| factorization.
| cov_type : str, optional
| See `regression.linear_model.RegressionResults` for a description
| of the available covariance estimators.
| cov_kwds : list or None, optional
| See `linear_model.RegressionResults.get_robustcov_results` for a
| description required keywords for alternative covariance
| estimators.
| use_t : bool, optional
| Flag indicating to use the Student's t distribution when computing
| p-values. Default behavior depends on cov_type. See
| `linear_model.RegressionResults.get_robustcov_results` for
| implementation details.
| **kwargs
| Additional keyword arguments that contain information used when
| constructing a model using the formula interface.
|
| Returns
| -------
| RegressionResults
| The model estimation results.
|
| See Also
| --------
| RegressionResults
| The results container.
| RegressionResults.get_robustcov_results
| A method to change the covariance estimator used when fitting the
| model.
|
| Notes
| -----
| The fit method uses the pseudoinverse of the design/exogenous variables
| to solve the least squares minimization.
|
| get_distribution(self, params, scale, exog=None, dist_class=None)
| Construct a random number generator for the predictive distribution.
|
| Parameters
| ----------
| params : array_like
| The model parameters (regression coefficients).
| scale : scalar
| The variance parameter.
| exog : array_like
| The predictor variable matrix.
| dist_class : class
| A random number generator class. Must take 'loc' and 'scale'
| as arguments and return a random number generator implementing
| an ``rvs`` method for simulating random values. Defaults to normal.
|
| Returns
| -------
| gen
| Frozen random number generator object with mean and variance
| determined by the fitted linear model. Use the ``rvs`` method
| to generate random values.
|
| Notes
| -----
| Due to the behavior of ``scipy.stats.distributions objects``,
| the returned random number generator must be called with
| ``gen.rvs(n)`` where ``n`` is the number of observations in
| the data set used to fit the model. If any other value is
| used for ``n``, misleading results will be produced.
|
| initialize(self)
| Initialize model components.
|
| predict(self, params, exog=None)
| Return linear predicted values from a design matrix.
|
| Parameters
| ----------
| params : array_like
| Parameters of a linear model.
| exog : array_like, optional
| Design / exogenous data. Model exog is used if None.
|
| Returns
| -------
| array_like
| An array of fitted values.
|
| Notes
| -----
| If the model has not yet been fit, params is not optional.
|
| ----------------------------------------------------------------------
| Data descriptors inherited from RegressionModel:
|
| df_model
| The model degree of freedom.
|
| The dof is defined as the rank of the regressor matrix minus 1 if a
| constant is included.
|
| df_resid
| The residual degree of freedom.
|
| The dof is defined as the number of observations minus the rank of
| the regressor matrix.
|
| ----------------------------------------------------------------------
| Methods inherited from statsmodels.base.model.LikelihoodModel:
|
| information(self, params)
| Fisher information matrix of model.
|
| Returns -1 * Hessian of the log-likelihood evaluated at params.
|
| Parameters
| ----------
| params : ndarray
| The model parameters.
|
| ----------------------------------------------------------------------
| Class methods inherited from statsmodels.base.model.Model:
|
| from_formula(formula, data, subset=None, drop_cols=None, *args, **kwargs) from builtins.type
| Create a Model from a formula and dataframe.
|
| Parameters
| ----------
| formula : str or generic Formula object
| The formula specifying the model.
| data : array_like
| The data for the model. See Notes.
| subset : array_like
| An array-like object of booleans, integers, or index values that
| indicate the subset of df to use in the model. Assumes df is a
| `pandas.DataFrame`.
| drop_cols : array_like
| Columns to drop from the design matrix. Cannot be used to
| drop terms involving categoricals.
| *args
| Additional positional argument that are passed to the model.
| **kwargs
| These are passed to the model with one exception. The
| ``eval_env`` keyword is passed to patsy. It can be either a
| :class:`patsy:patsy.EvalEnvironment` object or an integer
| indicating the depth of the namespace to use. For example, the
| default ``eval_env=0`` uses the calling namespace. If you wish
| to use a "clean" environment set ``eval_env=-1``.
|
| Returns
| -------
| model
| The model instance.
|
| Notes
| -----
| data must define __getitem__ with the keys in the formula terms
| args and kwargs are passed on to the model instantiation. E.g.,
| a numpy structured or rec array, a dictionary, or a pandas DataFrame.
|
| ----------------------------------------------------------------------
| Readonly properties inherited from statsmodels.base.model.Model:
|
| endog_names
| Names of endogenous variables.
|
| exog_names
| Names of exogenous variables.
|
| ----------------------------------------------------------------------
| Data descriptors inherited from statsmodels.base.model.Model:
|
| __dict__
| dictionary for instance variables (if defined)
|
| __weakref__
| list of weak references to the object (if defined)
These 4 implementations each have very different syntaxes for usage, and each return the fitted regression coefficients in different ways. We’ll see how this works when we apply them to simulated data.
Part 2#
Create some fake linear data. That is, create two lists of numbers \(X\) and \(Y\) that may or may not be linearly related. Make sure they are not identical and also not completely unrelated or the results will not be that interesting.
np.random.seed(12345)
N = 100
X = st.uniform.rvs(size=(N)) * 10 - 5
betaTrue = 4
intercept = 5
Y = betaTrue * X + intercept + st.norm.rvs(size=(N))
fig, ax = plt.subplots(1, 1, figsize=(12, 5))
_ = ax.scatter(X, Y)
_ = ax.set_xlabel("X")
_ = ax.set_ylabel("Y")
_ = fig.tight_layout()
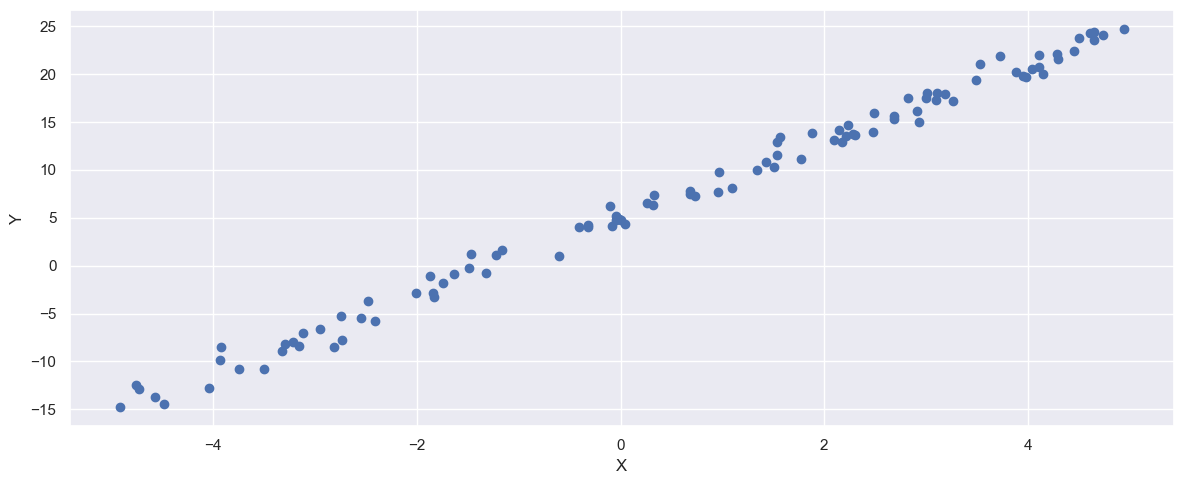
Part 3#
Run each of the above functions and examine their output. Answer the following for each function:
How can you extract the regression coefficients?
How can you get the residuals?
Which methods report “error” estimates in the coefficients?
How easy is this method to use?
Does this method fit the intercept (\(\beta_0\))?
np.polyfit#
Starting with np.polyfit, we see from the documentation that we put in our covariates, X, then the response variable, Y, followed by the degree of the polynomial we want to fit. In this case, we want to fit a line, so the degree is 1. Looking at the output, we can see that the function returns the fitted coefficients in order from the highest degree term to the lowest (in this case, the slope then the intercept).
We cannot directly get the residuals, but looking at the documentation, we see that there is a full keyword that outputs more information about the fitting process, including the sum of the squared residuals. However, we will not get the other error information that other methods will produce.
What this function lacks in sophistication it makes up for with simplicity. If you just need a line fit quickly, this is easy to use and already included in numpy.
This method fits the intercept by default.
coeffs = np.polyfit(X, Y, deg=1)
print(f"The fitted coeffs are {coeffs}")
coeffs, residuals, rank, singular_values, rcond = np.polyfit(X, Y, 1, full=True)
print(f"The sum of squared residuals is {residuals}")
The fitted coeffs are [4.0118807 5.03952838]
The sum of squared residuals is [95.30037147]
scipy.stats.linregress#
Moving on to scipy.stats.linregress, we see that the syntax is similar to np.polyfit, but a degree doesn’t need to be specified because (as the name suggests), this method only fits linear functions. Unlike np.polyfit, the documentation notes that the output of this method is a LinregressResult object that has several attributes containing the information we might want, like the slope and intercept, the Pearson correlation coefficient, and the standard errors in the estimates.
Again, we cannot directly get the residuals as output, but we can use the fitted coefficients to calculate them.
This method is relatively easy to use, the only difficulty may be in the unusual structure of the output.
This method fits the intercept automatically.
res = st.linregress(X, Y)
print(f"R-squared: {res.rvalue**2:.6f}")
## Following the example in the documentation, we can calculate the 95% confidence
## intervals in the estimates using the standard error information!
tinv = lambda p, df: abs(st.t.ppf(p/2, df)) ## This is a "lambda" function, which is
## a simple syntax for short function definitions
ts = tinv(0.05, len(X)-2)
print(f"slope (95%): {res.slope:.6f} +/- {ts*res.stderr:.6f}")
print(f"intercept (95%): {res.intercept:.6f} +/- {ts*res.intercept_stderr:.6f}")
R-squared: 0.992601
slope (95%): 4.011881 +/- 0.069436
intercept (95%): 5.039528 +/- 0.199360
fig, ax = plt.subplots(1, 1, figsize=(12, 5))
_ = ax.scatter(X, Y, label='Data')
_ = ax.plot(X, res.intercept + res.slope * X, color='r', label='Linear Fit')
_ = ax.legend()
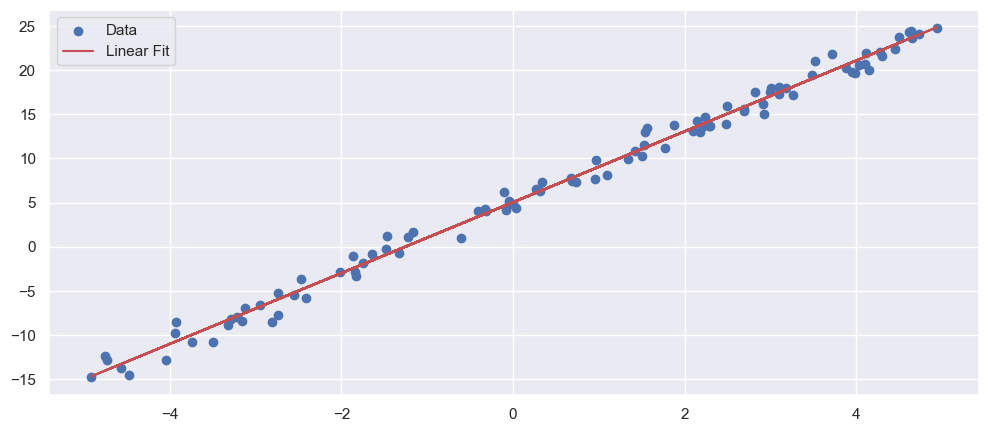
sklearn.linear_model.LinearRegression#
The next two methods are similar in that they make use of Python’s object-oriented syntax, which you can learn more about by looking at the tutorial section on Classes. For now, it will suffice to follow the examples here. The gist is that we first need to initialize a LinearRegression object, which will look like a normal function call, but will generate an instance of a LinearRegression-type object as output. This instance can then be used to fit the data and it will contain the outputs that we seek.
In this way, the coefficients are accessed similarly to st.linregress, where they are stored as attributes in an object. Unlike the LinregressResult object, the LinearRegression object also has methods like predict which we can use to calculate residuals quickly, as shown below.
Unlike st.linregress and statsmodels.api.OLS, the sklearn.linear_model.LinearRegression object will not generate traditional error calculations.
This method is definitely somewhat harder to get used to than the previous two, but this type of syntax is more common in advanced data science packages, especially machine learning and neural networks.
This method fits the intercept by default.
from sklearn.linear_model import LinearRegression as skLinReg ## Notice the import syntax.
X = X.reshape(-1, 1) ## Adds a dimension to the array (makes X & Y column vectors)
Y = Y.reshape(-1, 1)
linRegObj = skLinReg() ## Instantiate the object
linRegObj.fit(X, Y) ## Fit the linear model
beta1 = linRegObj.coef_[0, 0] ## We access the slope via the attribute `coef_`
beta0 = linRegObj.intercept_[0]
print(f"The fitted line is {beta1:.2f}X + {beta0:.2f}")
X_pred = linRegObj.predict(X)
resids = Y - X_pred
The fitted line is 4.01X + 5.04
fig, ax = plt.subplots(1, 1, figsize=(12, 5))
_ = ax.hist(resids, bins=20)
_ = ax.set_xlabel(r"Residual, $Y - \hat{Y}$")
_ = ax.set_ylabel("Count")
_ = fig.tight_layout()
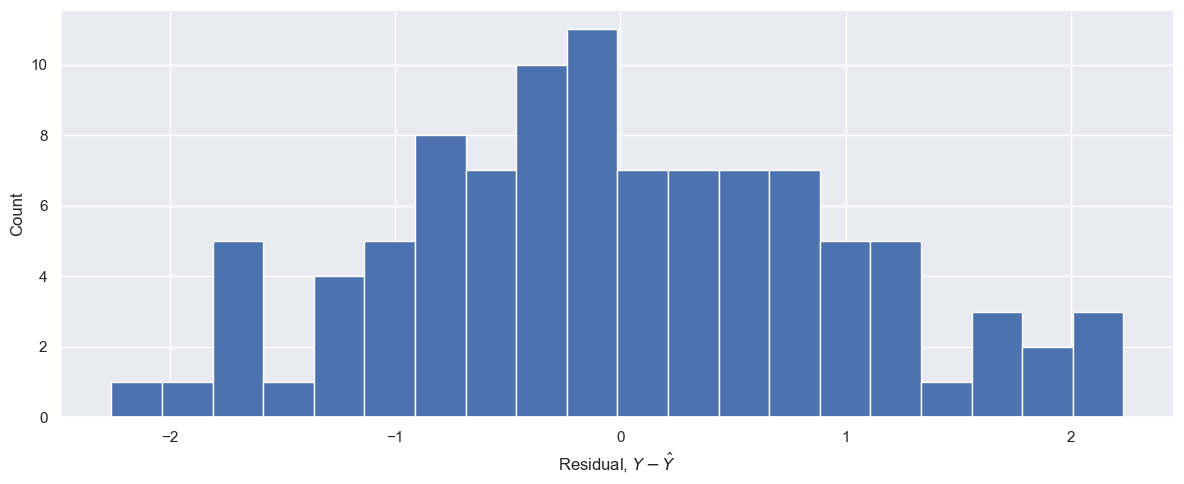
statsmodels.api.OLS#
Finally, we will look at the statsmodels.api.OLS method. This is the most advanced and complicated method of those we’ll examine, but it is also the most comprehensive. The statsmodels package is designed to replicate traditional statistics packages, and so it performs many standard analyses and contains many standard quantities by default. This is shown with the summary method below, where we see a variety of statistics related to the fit. However, navigating these various terms and objects can make this hard for beginners to use. It’s worth noting the different usage syntax especially.
Accessing the different outputs is done similarly to the previous two methods, but there are significantly more attributes and methods to sort through. The fitted coefficients can be recovered by accessing the params attribute of the results object, as shown below. The standard errors are found in the bse attribute.
The residuals are not stored in the results object, but similarly to the sklearn fitter, the results object has a predict method that can be use to quickly generate the model’s predictions, and thus its residuals.
This method does not fit the intercept by default, which is why we had to add a column to our covariates. (A column of constants can then have its “slope” fit, which will correspond to the intercept.)
import statsmodels.api as sm
smX = sm.add_constant(X) ## In order to fit an intercept term we need to
## add a column of ones to the covariates.
# print(smX)
model = sm.OLS(Y, smX) ## Note that the inputs are reversed compared to the other methods!
results = model.fit()
print(results.params) ## The coefficients are in the `params` attribute of the results object
print(results.summary())
print(f"\n\nThe standard errors can be accessed here: {results.bse}")
[5.03952838 4.0118807 ]
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.993
Model: OLS Adj. R-squared: 0.993
Method: Least Squares F-statistic: 1.315e+04
Date: Tue, 21 Mar 2023 Prob (F-statistic): 3.14e-106
Time: 16:29:01 Log-Likelihood: -139.49
No. Observations: 100 AIC: 283.0
Df Residuals: 98 BIC: 288.2
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 5.0395 0.100 50.164 0.000 4.840 5.239
x1 4.0119 0.035 114.658 0.000 3.942 4.081
==============================================================================
Omnibus: 0.894 Durbin-Watson: 1.951
Prob(Omnibus): 0.640 Jarque-Bera (JB): 0.966
Skew: 0.130 Prob(JB): 0.617
Kurtosis: 2.595 Cond. No. 2.94
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
The standard errors can be accessed here: [0.10046015 0.03498987]